赔率计算与凯利公式应用分析
在博彩中,赔率与概率之间存在着密切的关系,了解这一关系对于制定有效的投注策略至关重要。以下将详细解释赔率计算的原理及其相关公式,特别是凯利公式的应用。
一、赔率与概率的关系
赔率可以通过以下公式计算:

其中,百分比概率是由博彩公司分析师通过各种因素得出的预期概率,赔付率是博彩公司的投注返还率。
从上述公式可以推导出:
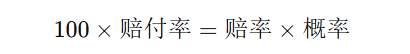
这意味着,赔率、概率和赔付率之间存在固定的数学关系。博彩公司根据这些数据来设置和调整投注赔率。
二、赔率转换
在实际应用中,我们经常需要根据不同的赔付率对赔率进行转换。为了保证百分比概率保持不变,可以使用以下公式进行转换:

这种转换方法确保了在不同赔率和赔付率条件下,概率保持一致。
三、返还率计算
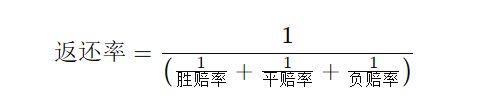
返还率是指在多次投注中,玩家期望从投注中得到的平均回报比例。它可以通过以下公式计算:
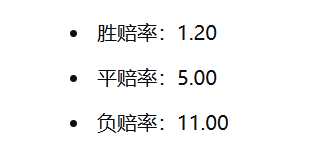
以尤文图斯对卡利亚里的比赛为例,假设威廉·希尔提供的赔率为:
根据上述公式,返还率的计算如下:
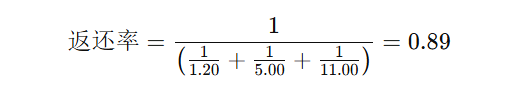
这个返还率表示,如果在长期内进行大量相同的投注,平均回报率为89%。
四、凯利公式
凯利公式用于计算最优投注金额,以最大化长期利润,并减少资金波动风险。其计算公式为:
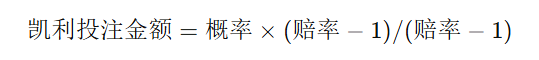
凯利的核心思想是,在给定概率的情况下,合理分配投注资金以达到最优回报。
以尤文图斯的胜赔率为例:

根据凯利公式:
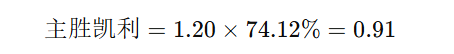
这表示,凯利公式建议的投注比例是0.91,也就是用91%的资金投注于尤文图斯获胜的选项。
五、标准差与方差
在统计分析中,标准差(Standard Deviation,σ)是用来衡量数据分布的离散程度的工具。标准差越高,表示数据的波动越大,越不精确;标准差越低,数据的稳定性越高。
标准差的计算公式为:
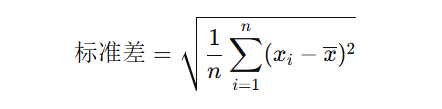

方差是标准差的平方,表示数据偏离均值的程度。标准差和方差是评估数据波动性的重要工具。
在Excel中,可以使用“STDEV”函数来计算样本的标准差。